Racks and Tubes: Short Division

Materials
- A tray which holds:
Seven test tube holders 
3 white for the groups of units
3 grey for the groups of hundreds.
3 grey for the groups of hundreds
Each holder has ten test tubes and each test tube holds 10 beads of the relevant hierarchical colors from units to millions.
                       
- Seven dishes – colored on the outside to correspond to the colors of the holders (groups) and on the inside to correspond to the colors of the bead (hierarchical).

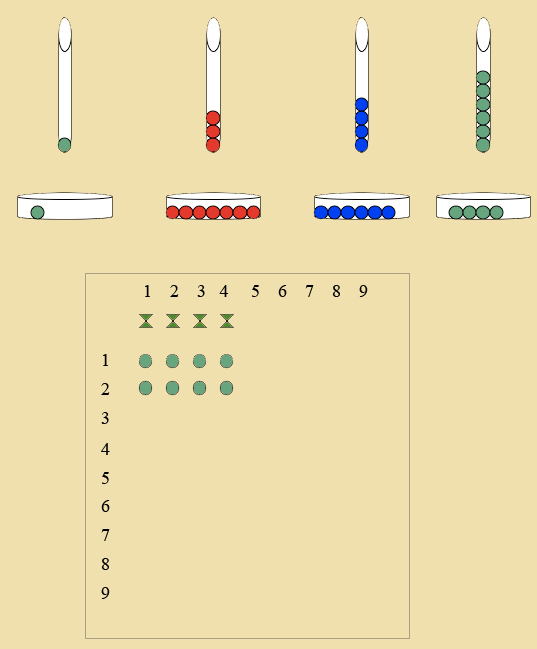
- Unit division board with nine green skittles


Presentation

Introduction

1. Have the child bring over the material.
2. Introduce the beads to the child.
3. Count how many beads are in the tubes with the child. Notice that each tube has ten beads.
4. Introduce the new board to the child.
5. Write a division problem on the paper:
   
   
   
6. Introduce the new way of writing a division problem.
7. Read the equation with the child.
8. Take out the tubes for the thousands, hundreds, ten, and units and place them in front of the tray of tubes.
9. You will now make the dividend with the beads. Take out 9 thousands (count each as you do) and place it in the appropriate dish in front of the thousand bead tubes.
10. Do the same for the hundreds, tens, and units.
11. Ask the child what the divisor is in the equation. (4)
12. Have the child place 4 skittles at the top of the board.
13. Remind the child that in division we always start with the thousands.
14. Have the child give each skittle a thousand bead until there is only one left.
15. Count how many thousands one skittle got: 2 (thousands)
16. Have the child record this by placing it as shown below:
    
    






17. Clear the board by placing the 8 beads back into the tube.
18. Place the last thousand bead in the hundred dish.
19. Ask the child, by looking at the hundred dish if we can share these beads. No, because you need to change the thousand into ten hundreds.
20. Have the child change the thousand bead into 10 hundreds.
21. Replace the tube of thousand beads and the dish onto the tray and out of the way.
22. Share out the hundred beads as you had for the thousand beads.
23. Repeat in the above steps for the hundreds, tens, and units.
    
    

Exercice
The child works as shown in the presentation. 

Presentation 2
When the child understand this process, you can show him on paper that his work with the materials actually is the written process of division:

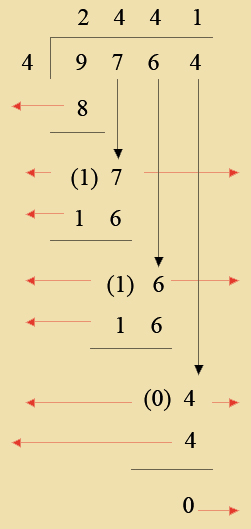
4 x 2 is shown on the board with 8 beads
1 is what you have after clearing the board		17 is how many hundred beadyou have after you change
4 x 4 is shown on the board with 16 beads
1 is what you have after clearing the board		16 is how many tens you have after changing the 100 bead
4 x 4 is shown on the board with 16 beads
0 is what you have after clearing the board		4 is how many units you have to share with the four skittles
4 x 1 is shown on the board with 4 beads
		0 is how many unit beads you have left after sharing 4 beads with each skittle

Purpose

Direct
To help the child understand the techniques of distributive division and to lead to abstraction.

Control of Error
The Directress and the child’s own ability

Age
5 1/2 – 6 years onwards

Questions, Comments ?

Share your experiences in the Forum